2. Beschleunigender Fortschritt
2.2 Moore's Law
Kommen wir jetzt zum Kern dieses Kapitels, dem Fortschritt. Dieser ist nämlich ebenfalls ein Beispiel für exponentielles Wachstum.
Wir beginnen die Betrachtung mit einem Spezialfall: „Moore's Law“, zu Deutsch „Mooresches Gesetz“. Dieses beschreibt, wie schnell Computerchips besser/komplexer werden.
Moore's Law besagt, dass sich die Anzahl der Transistoren* je Computerchip etwa alle 2 Jahre verdoppelt.
Viele positive Rückkopplungen in den Herstellungsprozessen haben Moore zu dieser Faustregel geführt. Sie hat sich so gut bewahrheitet, dass sie inzwischen als "Gesetz" bezeichnet wird. In gewisser Weise wurde es auch eine selbsterfüllende Prophezeiung, weil die gesamte Industrie diese Zielmarken akzeptiert und ihre Planung daran ausgerichtet hat.
Wir wollen uns aber gar nicht genauer damit beschäftigen, warum die Transistorzahl exponentiell wächst. Stattdessen wollen wir uns wieder ansehen, wo die Grenzen dieser Wachstumsfunktion liegen. Wann kann sich die Transistorzahl je Chip nicht mehr verdoppeln?
Es scheint, als wären wir bereits erstaunlich nah an diesem Punkt:
Aktuell sind wir in der Lage, 3nm (Nanometer) große Transistoren herzustellen. Transistoren bestehen aus Silizium, und ein Siliziummolekül ist etwa 0,2nm groß. Transistoren sind also aktuell bereits so klein, dass sie nur noch wenige Moleküle dick sind (etwa 15).
Mit 4 weiteren Verdopplungen in 8 Jahren währen wir dann bei 4 Molekülen Dicke (bei 0,8nm Transistorgröße), und da wäre dann so langsam Schluss. In Wirklichkeit schrumpfen die Transistorgrößen aber auch gar nicht mehr so stark wie es für das Mooresche Gesetz nötig wäre (Faktor 1,4 alle 2 Jahre). Stattdessen haben die Hersteller angefangen, die Transistoren dichter anzuordnen und mehrere Chiplagen übereinander zu stapeln, den Chip also dreidimensional statt flach aufzubauen.[9]
Wie lange könnte das gut gehen? Es hängt im Wesentlichen von der Wärmeentwicklung ab, wie viele Lagen übereinander gestapelt werden können. Denn ohne kleinere Strukturen verbrauchen mehr Transistoren auch entsprechend mehr Strom. Die Prozessoren von Laptops und Servern verbrauchen bereits jetzt viel Energie, sehr viel Spielraum bleibt dort also nicht. Nehmen wir einen Faktor von 8 an, dann haben wir auf diese Weise Raum für 3 weitere Verdopplungen.
Ohne komplette Technologiebrüche (wie optische Computer oder Quantencomputer) sind die Möglichkeiten dann ausgeschöpft.
In der aktuellen Grundtechnologie wären also vielleicht noch 7 Verdopplungen der Transistoren je Chip möglich. Damit hätte ein gleichgroßer Chip 2038 dann 128 (27) Mal so viele Transistoren wie heute. Er würde dabei aber auch acht Mal so viel Strom verbrauchen.
Der springende Punkt dafür, ob diese Vorhersage vom Ende der Chipbeschleunigung so eintreffen wird, ist die genannte Einschränkung: „Ohne komplette Technologiebrüche“. Wie wahrscheinlich ist das? Mit dem, was wir bisher über Moore's Law wissen, können wir hier nur mit den Schultern zucken und sagen „Wer weiß, ich bin kein Prophet“.
Da wir nicht direkt in die Zukunft sehen können, sehen wir stattdessen einmal in die Vergangenheit. Und versuchen, aus ihr die Zukunft abzuschätzen. Wie oft gab es schon Technologiebrüche bei Computern? In welchem Abstand sind sie aufgetreten?
Dafür gibt es eine schöne Grafik von Kurzweil, welche die Anzahl der Rechenoperationen pro Sekunde pro 1000$ von 1900 bis 2010 zeigt.
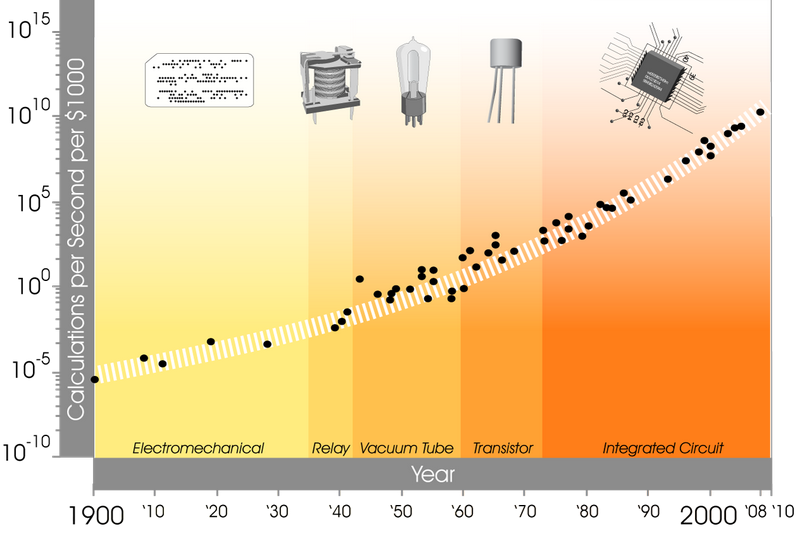
Wir haben hier die Technologiebrüche Elektromechanisch / Relay / Vacuumröhre / Transistor / Integrierte Schaltung (in der integrierten Schaltung ist der Transistor kein eigenständiges Bauteil mehr). Über diese Technologiebrüche hinweg ist der exponentielle Anstieg der Berechnungen für gleichbleibende Kosten erhalten geblieben. Auch in den folgenden 15 Jahren hat sich an diesem Anstieg nichts verändert.[11]
Kurzweil hat auf Grundlage dieses sich stets beschleunigenden Zuwachses an Rechenkapazität über Technologiebrüche hinweg eine ständige Beschleunigung des technologischen Fortschritts festgestellt.
Intuitiv möchte ich ihm da sofort zustimmen, einfach aufgrund dessen, was ich selbst erlebt habe und über die Vergangenheit weiß. Aber sich dabei nur den Zuwachs der Rechenleistung anzusehen, ist etwas wenig. Die Daten dafür reichen nur bis 1900 zurück, und vielleicht ist das exponentielle Wachstum nur ein spezieller Fall für diesen Zeitraum und für Rechenoperationen?
Wie aber können wir das anders sinnvoll messen? Einfach nur die Erfindungen zu zählen hilft ja nicht weiter: Man kann Erfindungen fast beliebig zusammenfassen oder aufspalten, und dadurch zu völlig unterschiedlichen Zahlen kommen.
Was ist technologischer Fortschritt, was sind Erfindungen? Es ist die Verbesserung der Mittel zum Lösen eines Problems. Sei das die effizientere Herstellung von etwas, Geräte zur besseren Messung, billigere Antriebskraft für Maschinen, Waffen für erfolgreicheren Kampf. Letztlich sind es alles Werkzeuge, die einem Zweck dienen. Und mit besseren Werkzeugen ist der Mensch effizienter. Eine Variante, den Fortschritt in Zahlen fassen zu können, ist also, sich die Effizienz oder Produktivität des Menschen anzusehen. Und das ist etwas, das bereits gemessen wird: Als Bruttoinlandsprodukt (BIP*), je Bevölkerung, um die Inflation bereinigt.
Auf der dafür bereitgestellten Datenbasis, hier ein Graph für Großbritannien für die Jahre 1000 bis 2022 (einfach, weil für dieses Land ab dem Jahr 1000 Daten bereit stehen, es eines der Entstehungsländer der wissenschaftlichen Revolution war, und seitdem durchgehend erfindungsmäßig auf der Höhe der Zeit war und ist):
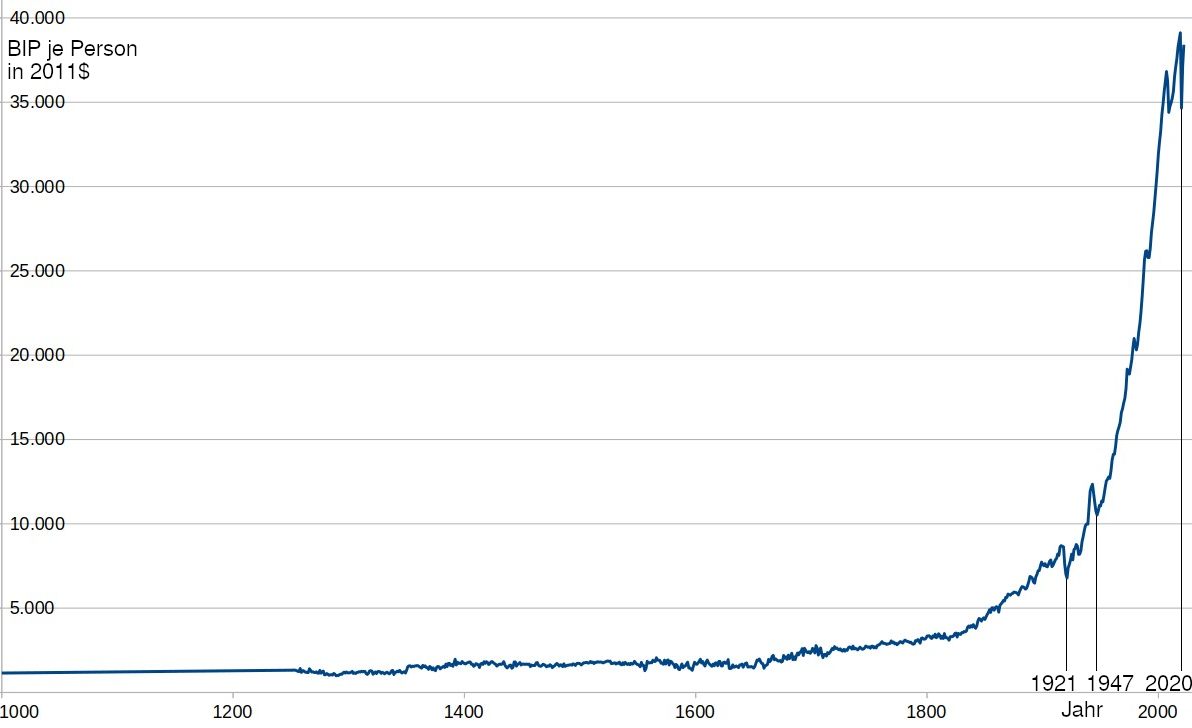
Ich denke, aufgrund dieses Graphen können wir Kurzweil recht geben und sagen: Ja, der technologische Fortschritt wird in der Tat immer schneller, er wächst exponentiell.
Wir können also davon ausgehen, dass es weitere Technologiebrüche geben und die Rechenleistung weiter exponentiell wachsen wird.
Und nicht nur diese, sondern Erfindungen im allgemeinen. Die Grenze dieses Wachstums wären entweder ein Zusammenbruch der Zivilisation, oder eine Annäherung an die Grenzen des physikalisch Möglichen. Letzteres ist aber bisher nicht absehbar, selbst auf Basis der bisher bekannten Naturgesetze.